วัดการประยุกต์ใช้ความรู้ซึ่งมีเนื้อหาตามสาระการเรียนรู้แกนกลางและสาระการเรียนรู้เพิ่มเติม กลุ่มสาระการเรียนรู้คณิตศาสตร์ (ฉบับปรับปรุง พ.ศ. 2560) ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551
โครงสร้างข้อสอบ
-
ข้อสอบ A-Level 61 Math1 วิชาคณิตศาสตร์ประยุกต์ 1 ประกอบด้วย 4 ส่วนคือ
- จำนวน: 15 - 17 ข้อ
-
ส่วนที่ 2 : สาระการวัดและเรขาคณิต
1) เรขาคณิตวิเคราะห์
2) เวกเตอร์ในสามมิติ
จำนวน: 3 - 5 ข้อ -
ส่วนที่ 3 : สาระสถิติและความน่าจะเป็น
1) สถิติ
2) การแจกแจงความน่าจะเป็นเบื้องต้น
3) หลักการนับเบื้องต้น
4) ความน่าจะเป็น
จำนวน: 6 - 8 ข้อ -
ส่วนที่ 4 : สาระแคลคูลัส
1) แคลคูลัสเบื้องต้น
จำนวน: 2 - 4 ข้อ -
ประเภทข้อสอบ ปรนัย 5 ตัวเลือก / ระบายคำตอบที่เป็นตัวเลข
ระยะเวลาที่ใช้สอบ 90 นาที
-
หมายเหตุ
1) ข้อสอบบางข้อมีการบูรณาการระหว่างเนื้อหา
2) ขอบเขตเนื้อหาของข้อสอบ สามารถศึกษาได้จาก เอกสารตัวชี้วัดและสาระการเรียนรู้แกนกลาง กลุ่มสาระการเรียนรู้คณิตศาสตร์ (ฉบับปรับปรุง พ.ศ. 2560) ตามหลักสูตรแกนกลางการศึกษาขั้นพื้นฐาน พุทธศักราช 2551 จาก เว็บไซต์สำนักงานคณะกรรมการการศึกษาขั้นพื้นฐาน กระทรวงศึกษาธิการ
จำนวนข้อ
ตัวอย่างข้อสอบ
-
ตัวอย่างที่ 1 รูปแบบปรนัย 5 ตัวเลือก 1 คำตอบ
บริษัทผลิตเครื่องดื่มแห่งหนึ่งวางแผนที่จะลดกำลังการผลิตสินค้าในแต่ละเดือน โดยจำนวนขวดของเครื่องดื่มที่จะผลิตในเดือนถัด ๆ ไป จะลดลงร้อยละ 3 ของจำนวนขวดของเครื่องดื่มที่ผลิตในเดือนก่อนหน้า ถ้าเดือนมกราคม 2565 บริษัทมียอดการผลิตเครื่องดื่มจำนวน 500,000 ขวด แล้วเดือนพฤศจิกายน 2565 บริษัทนี้จะมียอดการผลิตเครื่องดื่มกี่ขวด
คำตอบ
เฉลย/เหตุผลและแนวคิดในการตอบคำถาม

-
ตัวอย่างที่ 2 รูปแบบปรนัย 5 ตัวเลือก 1 คำตอบ
พิจารณาข้อความต่อไปนี้

คำตอบ
เฉลย/เหตุผลและแนวคิดในการตอบคำถาม
พิจารณาข้อความในแต่ละข้อได้ดังนี้

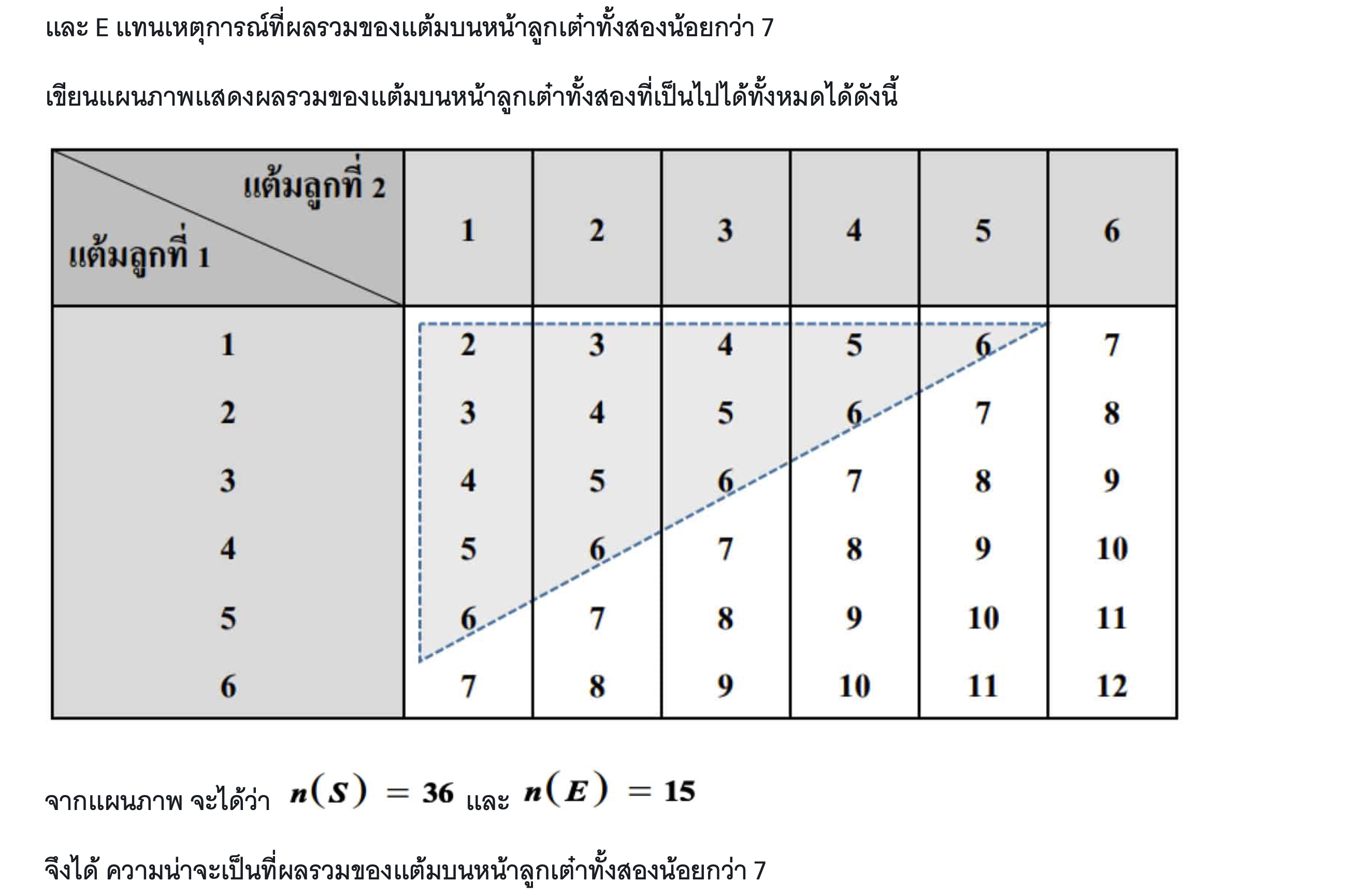

ดังนั้น ข้อที่ถูกต้อง คือ ตัวเลือก 2. ข้อความ ข) ถูกต้องเพียงข้อเดียวเท่านั้น
-
ตัวอย่างที่ 3 รูปแบบปรนัย 5 ตัวเลือก 1 คำตอบ
ให้
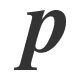 และ
และ 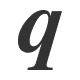 เป็นประพจน์
เป็นประพจน์
ถ้ารูปแบบของประพจน์
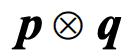 มีค่าความจริง แสดงดังตาราง
มีค่าความจริง แสดงดังตาราง
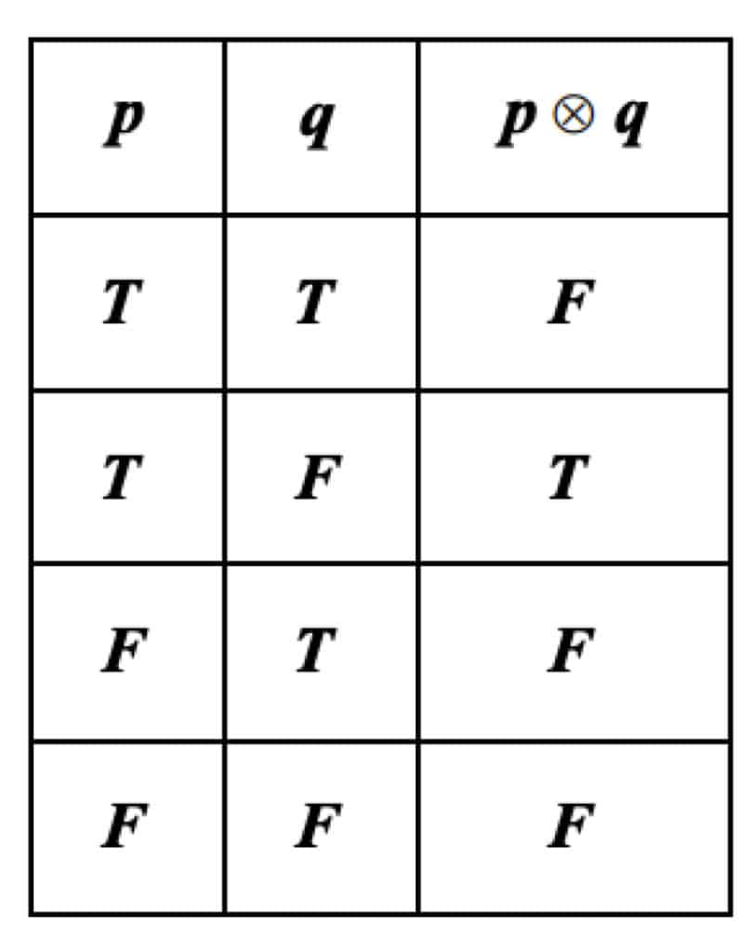
แล้ว
 (
(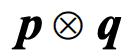 ) สมมูลกับรูปแบบของประพจน์ในข้อใด
) สมมูลกับรูปแบบของประพจน์ในข้อใด
คำตอบ
เฉลย/เหตุผลและแนวคิดในการตอบคำถาม
พิจารณาค่าความจริงของรูปแบบของประพจน์
 (
(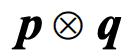 ) ได้ดังนี้
) ได้ดังนี้
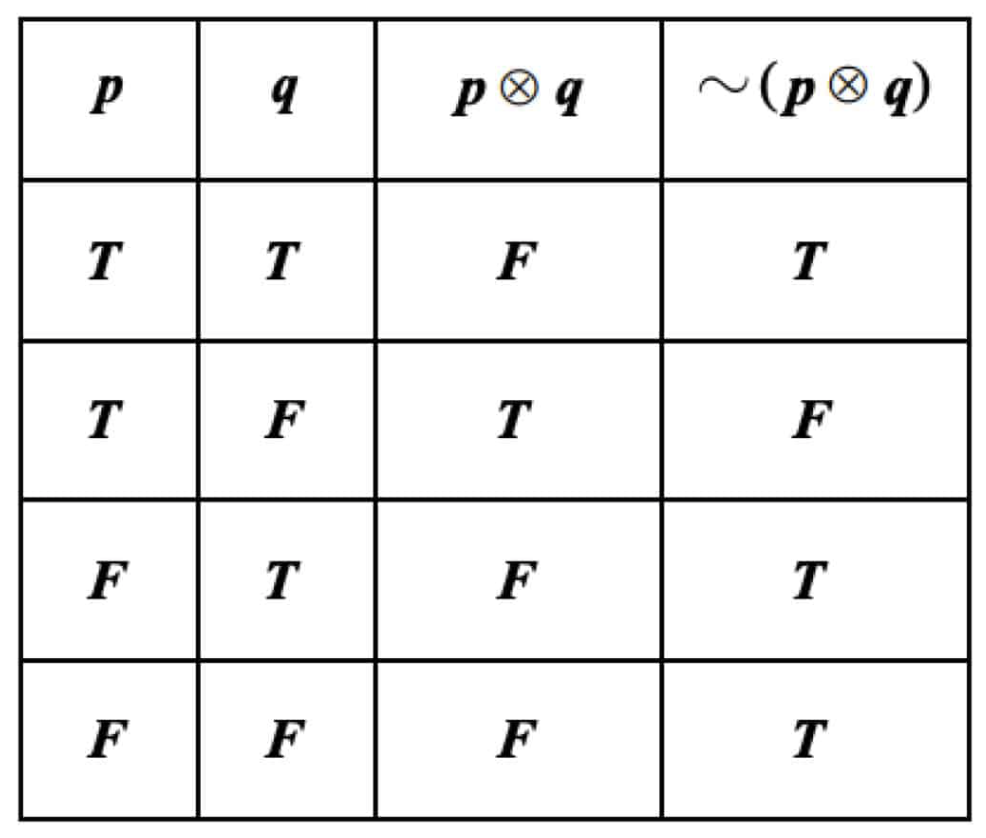
พิจารณาค่าความจริงของรูปแบบของประพจน์ในตัวเลือกแต่ละข้อได้ดังนี้
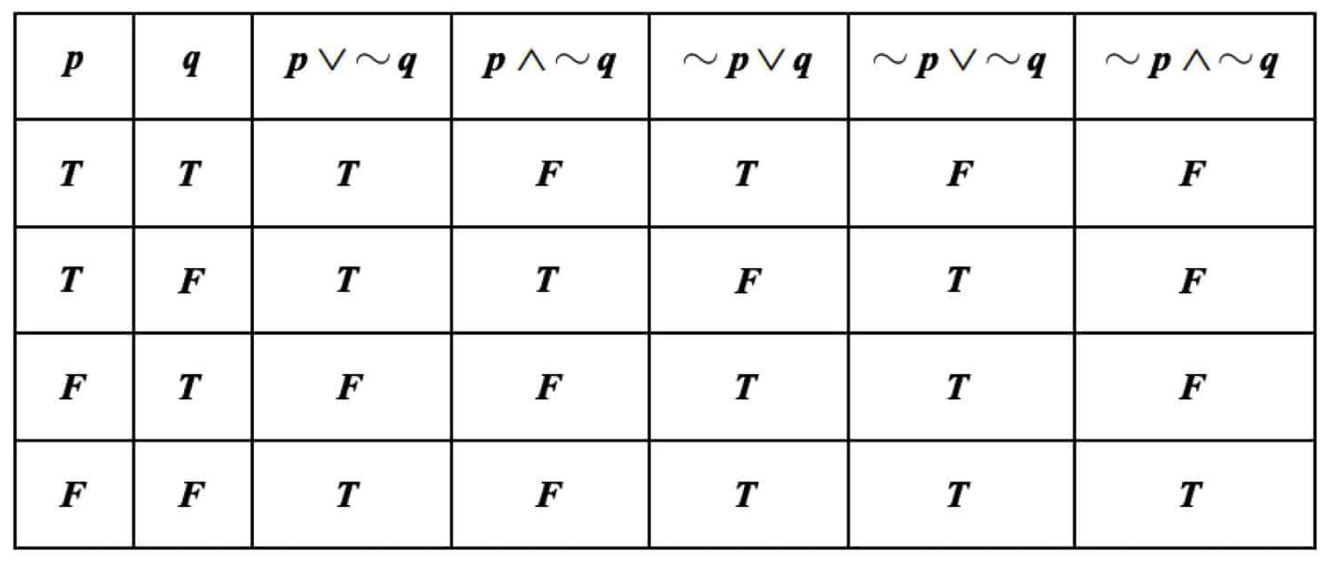
จากตารางค่าความจริง จะได้ว่า
 (
(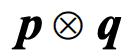 ) สมมูลกับ
) สมมูลกับ 

-
ตัวอย่างที่ 4 รูปแบบระบายคำตอบที่เป็นตัวเลข
เจ้าของฟิตเนสแห่งหนึ่งได้ทำการสำรวจกำไรต่อวัน พบว่า ฟังก์ชันแสดงกำไรต่อวัน
เมื่อมีผู้ใช้บริการ
คนต่อวัน เป็นฟังก์ชันพหุนามกำลังสอง โดยที่
- ในวันที่ไม่มีผู้ใช้บริการ จะขาดทุน 4,000 บาท
- ในวันที่มีผู้ใช้บริการ 10 คน จะมีรายได้เท่ากับต้นทุน
- ในวันที่มีผู้ใช้บริการ 30 คน จะได้กำไร 2,000 บาท
ฟิตเนสแห่งนี้จะมีกำไรต่อวันสูงสุดเท่ากับกี่บาท
เฉลย/เหตุผลและแนวคิดในการตอบคำถาม
2,250 บาท

-
ตัวอย่างที่ 5 รูปแบบระบายคำตอบที่เป็นตัวเลข
ให้จำนวนเชิงซ้อน z มีส่วนจินตภาพเป็น 124
ถ้า n เป็นจำนวนนับ ซึ่ง
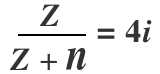
แล้ว n มีค่าเท่ากับเท่าใด
เฉลย/เหตุผลและแนวคิดในการตอบคำถาม












